Bueno, a sólo 8 kilómetros de altura.
Al monte Everest por ejemplo, que está aquí a lado. Bueno, al lado si lo comparamos con el espacio exterior, en una órbita baja. Bueno… que me habéis entendido a la primera.
Bien, la verdad es que este post es una excusa para compartir la siguiente foto: la tomó en 1997 el alpinista Ed Viesturs en la que era su quinta ascensión al Everest. Cuando le pilló el amanecer a 8700 metros, vio lo que recoge esta imagen: la sombra del propio monte Everest, perdiendose en el infinito.

Lamentablemente no encuentro la foto a más resolución, sería un fondo de pantalla o un poster para enmarcar legendario. Pinchando la imagen vais a la página de National Geographic.
Insisto en lo que no hace falta insistir: la foto es espectacular, me parece una verdadera pasada, por todo lo que supone su contexto, por su unicidad, por la propia belleza plástica de la imagen, y también, por unas cuantas lecciones sobre geometría y ciencia general que podemos aprender: esta foto, en si misma, demuestra que la Tierra no es plana.
Bien, todo esto viene de una pregunta que me vengo haciendo desde pequeño: ¿A qué altura hay que ascender para que se haga evidente la curvatura de la Tierra? Partimos de que la curvatura de la Tierra, de por sí, no es un concepto intuitivo. Con todo, y a pesar de lo comúnmente creido, los antiguos navegantes ya eran conscientes de este fenómeno (según navegaban al norte o al sur, unas estrellas u otras desaparecían del cielo nocturno), e incluso Erastótenes supo deducir con una precisión acojonante el radio terrestre. El hecho de que Colón llegara a las ‘Indias’ navegando hacia el este, o que Magallanes y Elcano circunnavegasen el globo, solo demostraba de forma práctica algo ya sabido entre gente medianamente ilustrada, y probablemente para cualquiera que se hubiera planteado seriamente la pregunta. Me imagino que preguntarse si la población general en el medievo era consciente o no de si vivían encima de un disco o de una esfera es concederles el beneficio de suponer que a lo largo de sus vidas llegaban a plantearse alguna vez dicha pregunta: supongo que bastante tenían ya con conseguir algo de cosecha y no morir por la peste… En fin, tal vez todo esto nos resulte ya solo anecdótico, si no fuera porque a estas alturas sigue existiendo la Flat Earth Society. Si. No es coña. Pero vayamos al tema.
Como decía, la pregunta es ¿Hasta dónde hemos de subir para ver claramente la curvatura de la Tierra? Es evidente que a nivel del mar, a efectos prácticos el horizonte que vemos es indistinguible del que correspondería a un plano infinito. Por el contrario, las imágenes hechas desde una órbita baja (entre 200 y 400 Km) demuestran sin ambigüedades la curvatura de la Tierra. La curvatura de la Tierra, evidentementemente, aparece como un efecto gradual, y para más dificultad, la atmósfera distorsiona, oscurece y difumina el horizonte (características geográficas aparte), por lo que, claro está, no se puede decir una cifra exacta a partir de la cual se hace evidente dicha curvatura.
Por todo ello, antes de entrar a saco al tema permitidme antes recordaros brevemente un poco de geometría.
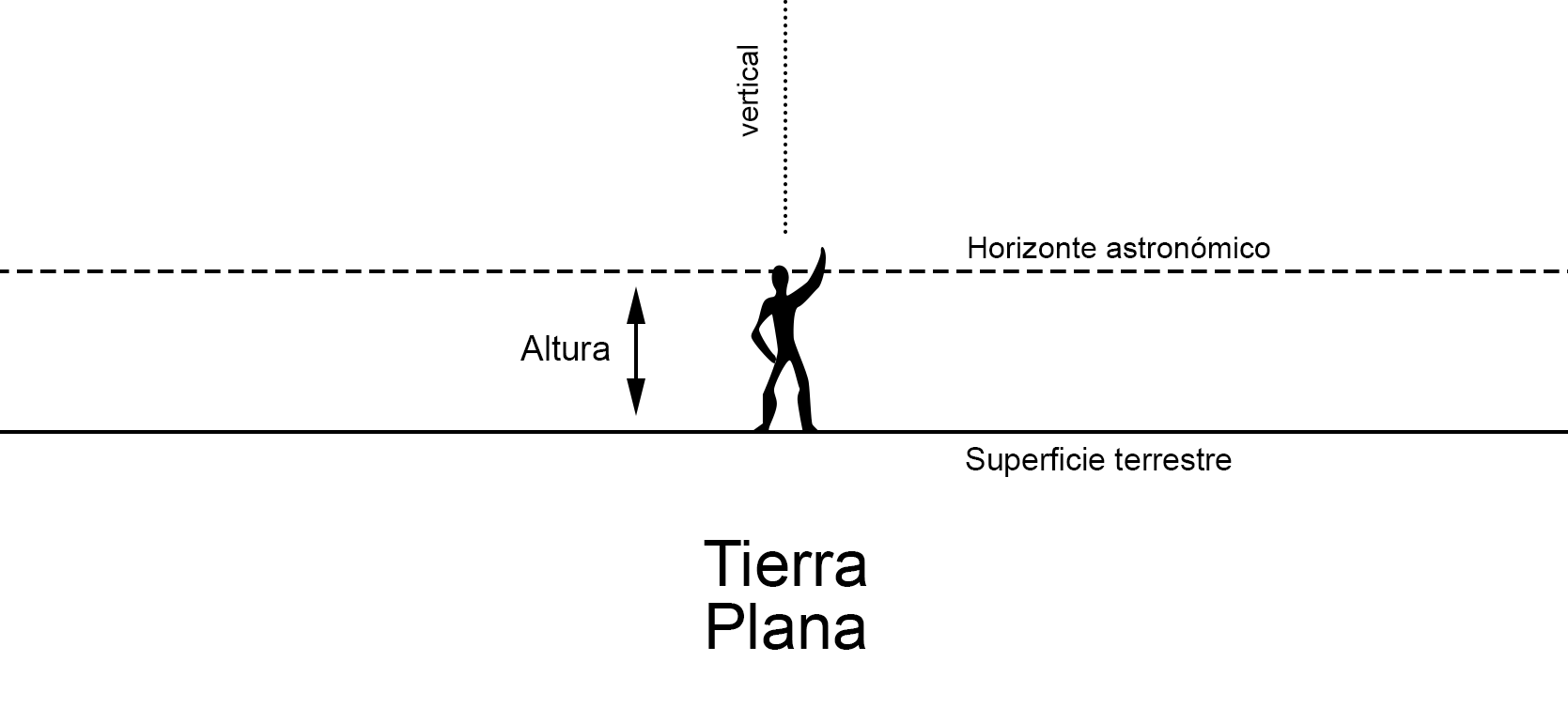
En una Tierra Plana e infinita, el horizonte astronómico, que es aquel que se aleja 90º de la vertical, y el geométrico (determinado por la superficie terrestre) coincidirían perfectamente, independientemente de la altura a la que nos encontremos sobre esta Tierra imaginaria. Esto se debe a que ambos elementos son paralelos, por lo que convergen en el infinito.
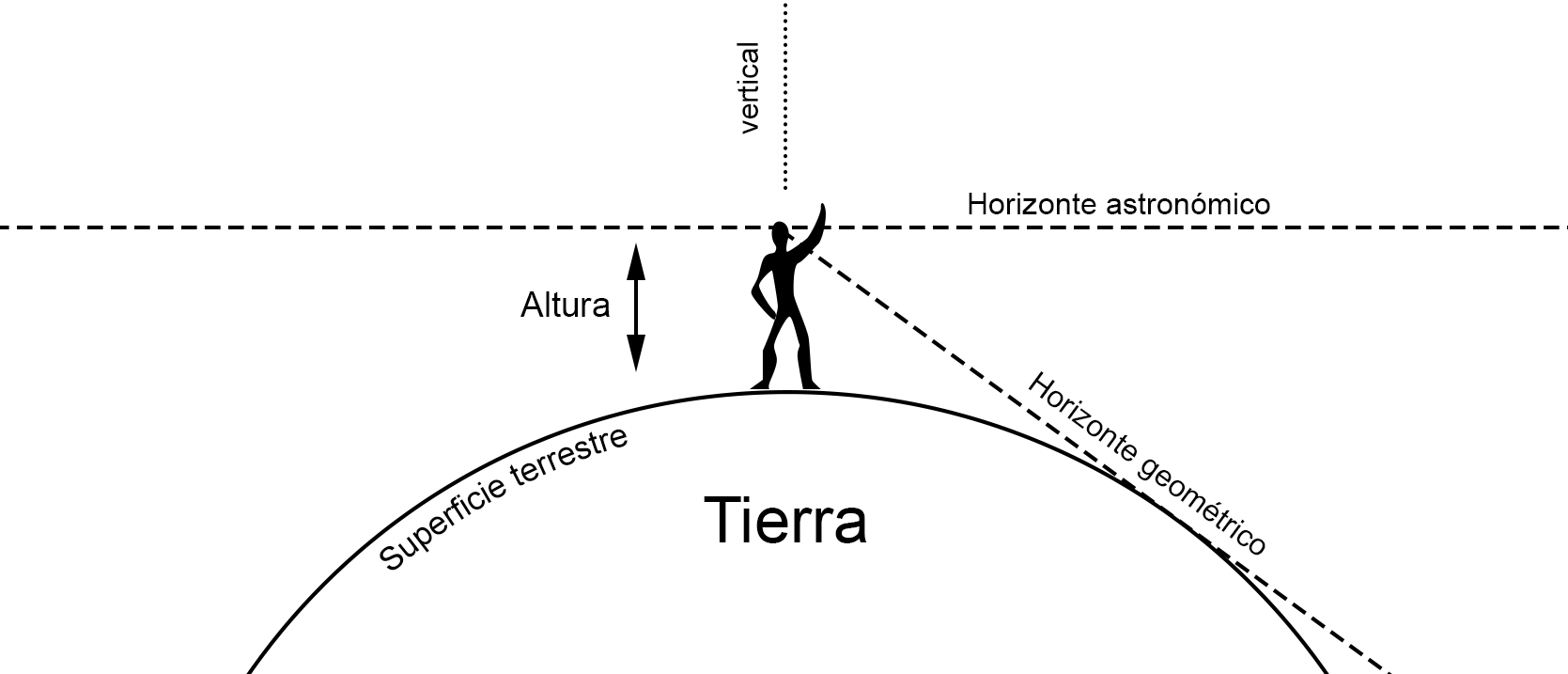
En una Tierra perfectamente esférica, el horizonte geométrico es una linea tangente a la superficie, uno de cuyos extremos depende de la altura a la que nos encontremos. Debido a esto, el horizonte geométrico y el astronómico solo coinciden en cota cero, esto es con nuestra cabeza sumergida en el agua hasta el nivel de los ojos.
A una altura pequeña, como la de una persona normal, la diferencia entre una Tierra esférica y una plana es insignificante. Pero en una Tierra esférica, tanto más ascendemos, tanto más van dejando los horizontes geométrico y astronómico de coincidir.
(…)
Pues bien, hagamos el experimento tirando de Google Earth. Me he plantado pilotando un F-16 (pulsando Ctrl+Alt+A dentro del programa) en la pista de aterrizaje del Aeropuerto de Málaga. Viene de puta madre porque entre los datos en pantalla de la cabina hay un horizonte artificial, que corresponde al astronómico, y nos permite compararlo con el real.

Me hallo al final de la pista, mirando hacia la costa. La altura sobre el nivel del mar es de tan solo 5 metros, y el horizonte astronómico (la linea 0) y el real coinciden perfectamente.
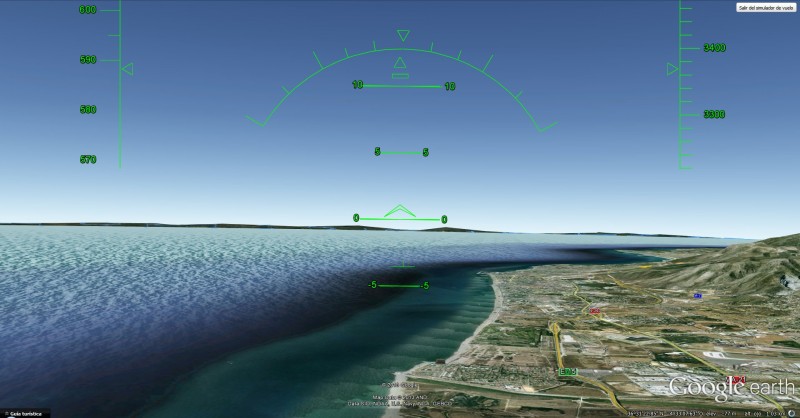
Sin embargo, a apenas un kilómetro de altura, horizonte astronómico y real han dejado de coincidir. Con todo, el efecto es solo perceptible con instrumentación (la diferencia no llega a un grado) y sería disimulado por la atmósfera, pero una persona observadora probablemente se hubiera dado cuenta de otro efecto: la costa africana es ahora visible, mientras no lo era desde la costa.
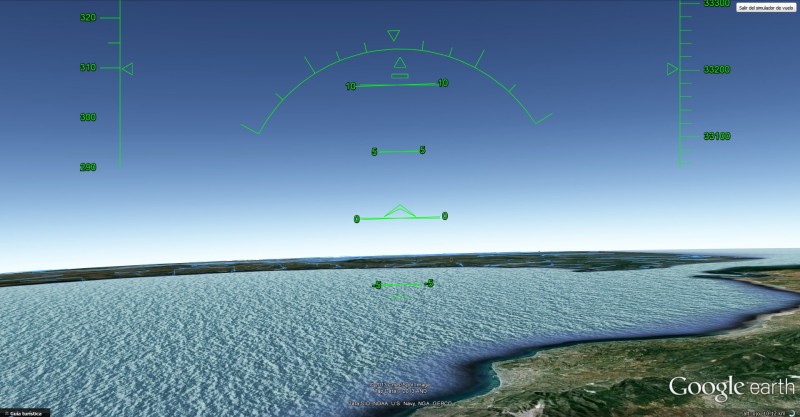
A la altura de un vuelo comercial (aprox. 11 km), el efecto, sin ser espectacular, está definitivamente marcado. No solo la visibilidad alcanza -idealmente- casi los 400 km, sino que la misma curvatura de la tierra se empieza a intuir, como que algo raro pasa. Lamentablemente desde las ventanillas de un avión no tenemos apenas visión del entorno, aunque es posible reconocer la curvatura tomando otras claves…
Algunas de esas claves las podemos encontrar en este efecto que tuve la fortuna de cazar en un vuelo de Málaga a Barcelona hace unos años.

Tranquilos, la distorsión del horizonte es fruto del ensamblaje del panorama, en la realidad la curvatura terrestre no es tan evidente. Pero las explicaciones, para la segunda parte ;)
Edición a 1 de Abril de 2018: Todavía no he publicado la mencionada segunda entrada, en buena parte debido a que el ‘debate’ sobre la Tierra Plana (si es que existe dicho debate), se nos ha ido de la mano a todos; debate que no existía cuando publiqué esta primera entrada y era más sosegado y calmado, y esto no era más que un ejercicio didáctico/divulgativo…
No obstante, si he escrito una entrada en Quora, respondiendo a algunas preguntas, que espero que os resulte interesante, hasta que publique la segunda (y tal vez tercera, y cuarta…) parte de esta serie.
¿Cómo se puede probar que el mundo es redondo para mí? ¿Cómo descubrieron los astrónomos de la antigüedad que la Tierra era redonda?
Espero que os resulte útil e interesante. Saludos!

Pingback: Bitacoras.com
No tenía ni idea de lo del F16 en el Google Earth, ¡qué pasada! :D
Jajaj, si sabía yo que quedaba alguien sin saberlo, nunca es mala ocasión para recordar lo del F16 ;)
Si la tierra fuera redonda, la prueba más contundente serían las fotitos de la NASA… Pero entonces, porque recurrir a todos estos análisis? No sera que ud tampoco le cree a la NASA?
Hola Rodrigo. Una prueba más contundente que esa (y otras que aparecerán en breve en la segunda parte de este artículo) y la más sencilla de comprobar, es el hecho de que los barcos desaparecen conforme se alejan en el horizonte, y las estrellas cambian según cambiamos de latitud. Hay otras demostraciones que requieren de nociones básicas sobre geometría, pero también se pueden comprobar facilmente. Y en un plano más amplio, hace falta fiarse de la razón y de las pruebas, no solo de nuestras impresiones y sentidos. Más que de la NASA (y me fio de ella), me fio de la ciencia y de la razón. Un saludo.
«es el hecho de que los barcos desaparecen conforme se alejan en el horizonte» La de los barcos esta refutada, si haces un zoom con un telescopio o una camara lo veras nuevamente. Lo de las estrellas es discutible. Si podras encontras argumentos en contra de la tierra plana analizas el polo sur
Vale. Pues haz la prueba. Vete a Málaga un día que haga buen tiempo (ni demasiado calor, ni brumas ni viento) y te subes al Castillo de Gibralfaro, que está a unos 130 metros de altura, y miras hacia el sur con unos prismáticos normalitos. Como digo, si hace bueno y te fijas, podrás ver algunas cumbres próximas de la costa africana, concretamente el Rif. Hasta aquí todo bien ¿verdad? Bien, terminada la visita, te bajas a la playa de La Malagueta y miras hacia el sur. ¿qué cantidad de montañas ves ahora? ¿las mismas?
yo desde Malaga, en la playa de la malagueta vi con un telescopio CEUTA a 71 millas…. a nivel del mar…. si quieres tengo fotos.
Pingback: Mientras peor, mejor (3 de 5): Internet, what have you done? | RIdP
La nasa miente. La gravedad es falsa.
La física y la física cuántica no es exacta.
Respeto el informe, mastique Y tragense que el hombre llegó a la luna también.
¿cómo demostraste que la física no es exacta?
La tierra es plana punto y no hay ninguna imagen que demuestre que es esférica ni en cámaras a 37 kilómetros puestas globos cualquiera puede coger una cámara de alta resolución o un telecopio y podar comprobar que nada se oculta en la imaginaria curvatura inexistente de la tierra
Yo he visto desde distintos puntos de Andalucia muchas ciudades de africa, todas a mas de 115 kilometros. Eso seria imposible en una tierra globo.
el que quiera fotos le puedo enviar, fueron mas de 20 dias con telescopio
Pingback: Puesta al día: mi trabajo de profesor en ESADA (y otras cosas) | RIdP
Disculpe, no logro encontrar la segunda parte ¿Cómo se llama? Me quedé muy interesado en la explicación que iba a dar
Hola Alan, nunca llegué a publicar la segunda parte (aunque sigo teniendo previsto publicarla algún día), en buena parte… porque el debate, si es que se le puede llamar así, se nos ha ido de las manos y dejó de ser divertido. No obstante publiqué un respuesta en Quora que puede servir como una especie de segunda parte de esta entrada; espero que te pueda resultar interesante:
https://es.quora.com/Cómo-se-puede-probar-que-el-mundo-es-redondo-para-mí-Cómo-descubrieron-los-astrónomos-de-la-antigüedad-que-la-Tierra-era-redonda/answer/Rufino-Herrera-García?nsrc=4&snid3=2220530069
Saludos!
Muchísimas gracias
La realidad es que hay pruebas lógicas de la tierra plana… Desde la logica a la biblia!
Saludos. La realidad es que son muy escasos los alegatos lógicos que apenas puedan sugerir la posibilidad de que la Tierra sea plana. Revisa los foros donde se explican la falsedad de los argumentos usados para que te des cuenta.
Tengo unas preguntas, 1)Menciona tres aspectos importantes que el piloto debe tomar en cuenta en un vuelo? 2)el avion es independiente a la rotacion de la tierra? 3)El avion debe descencer de altura constantemente?
Muy dudoso tu informe la fotos que valen son con mentes rectilineos aparte no hay fotos reales de la.tierra la nasa es una mentira
Tu argumento tiene menos base aún que el que yo diga que tú eres pura mentira, ya de que la NASA por lo menos son toneladas las pruebas de sus operaciones y sus resultados durante décadas, avalados por millones de personas del mundo entero. Que tú y un grupo de desorientados no quieran ver las pruebas no las hacen mentiras. Te reto a que le hagas una carta a tu nieto no nacido contándole tus creencias, para que cuando él, ya mayor, realice paseos espaciales se divierta un poco recordando en las absurdas creencias de su abuelo.